로지스틱 회귀
퍼셉트론은 클래스가 선형적으로 구분되지 않을 때, 절대 수렴할 수 없다.
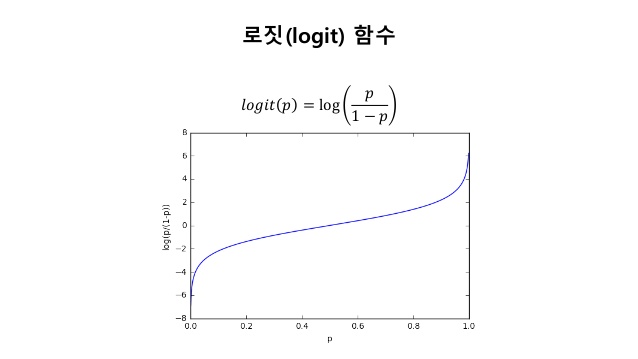
로지스틱 회귀(Logistic regression)은 선형 이진 분류에 더욱 강력하다.
(로지스틱 회귀는 회귀가 아닌 분류 모델이다)
로지스틱 회귀 이진 분류를 위한 선형 모델이지만, 다중 클래스 설정으로 일반화할 수 있다.
다항 로지스틱 회귀(multinomial logistic regression) 또는 소프트맥스 회귀(softmax regression)라고 부른다.

logit 와 Z의 선형 관계를 이용하면 logit(P(y=1)|x))=w0x0+w1x1+w2x2+ … + wmxm=w.Tx=Z 로 나타낼 수 있다.
import matplotlib.pyplot as plt
import numpy as np
def sigmoid(z):
return 1.0/(1.0+np.exp(-z))
z=np.arange(-7, 7, 0.1)
phi_z=sigmoid(z)
plt.plot(z,phi_z)
plt.axvline(0.0, color='k')
plt.ylim(-0.1, 1.1)
plt.xlabel('z')
plt.ylabel('$\phi (z)$')
plt.yticks([0.0, 0.5, 1.0])
ax=plt.gca()
ax.yaxis.grid(True)
plt.tight_layout()
plt.show()
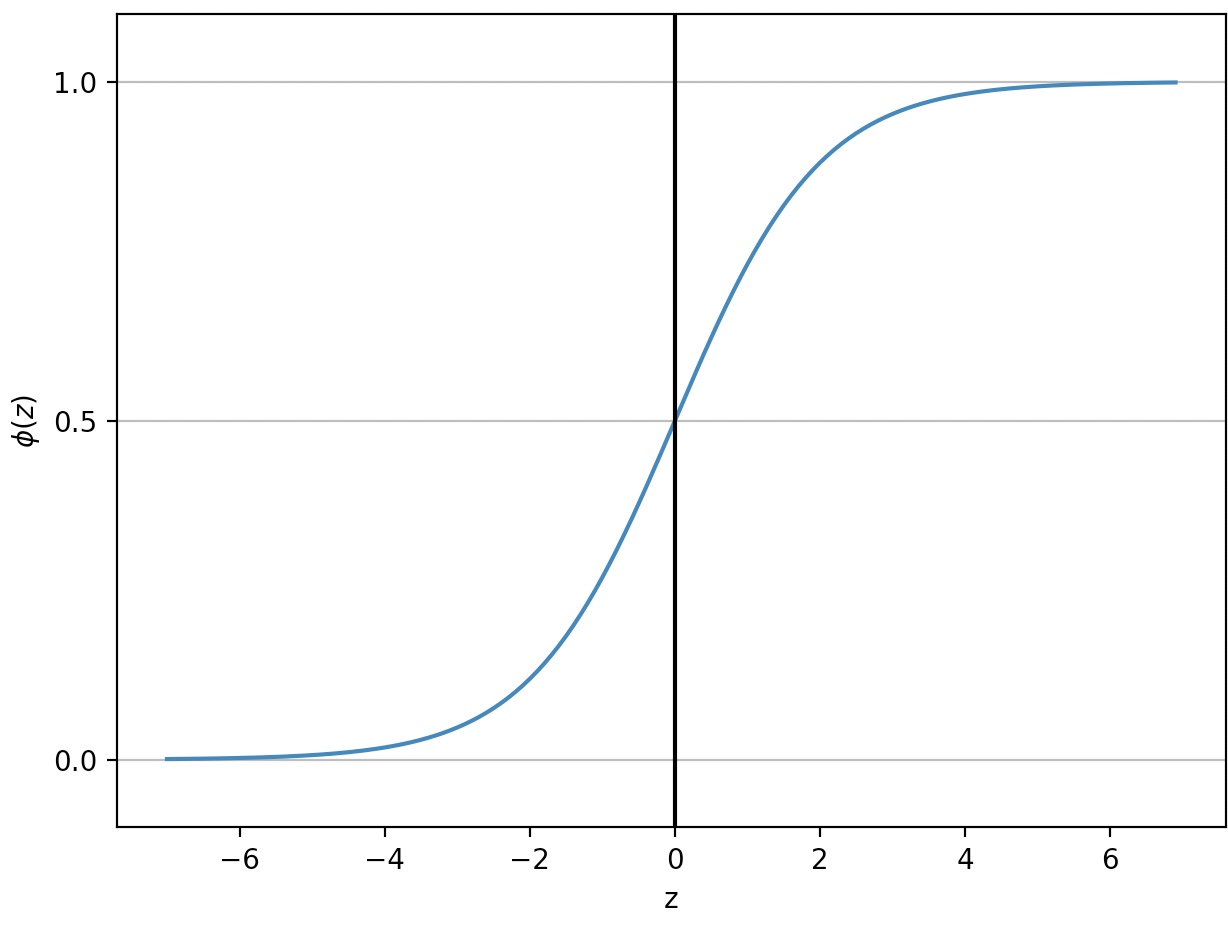
로지스틱 회귀에서는 위와 같은 시그모이드 함수를 활성화 함수로 사용한다.
로지스틱 함수는 클래스 레이블을 예측하는 것 외에 클래스에 소속될 확률을 추정하는데 유용하다.
로지스틱 함수의 가능도(Likelihood)
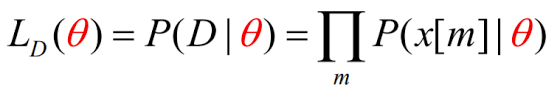
위의 가능도 함수에 로그(자연)함수를 취한 함수를 로그 기능도 함수라고 한다.
로그함수를 취함으로써 가능도가 매우 작을 때 발생하는 수치상의 언더플로(underflow)를 미연에 방지할 수 있다.
또한 계수의 곱을 계수의 곱으로 바꿀 수 있다.

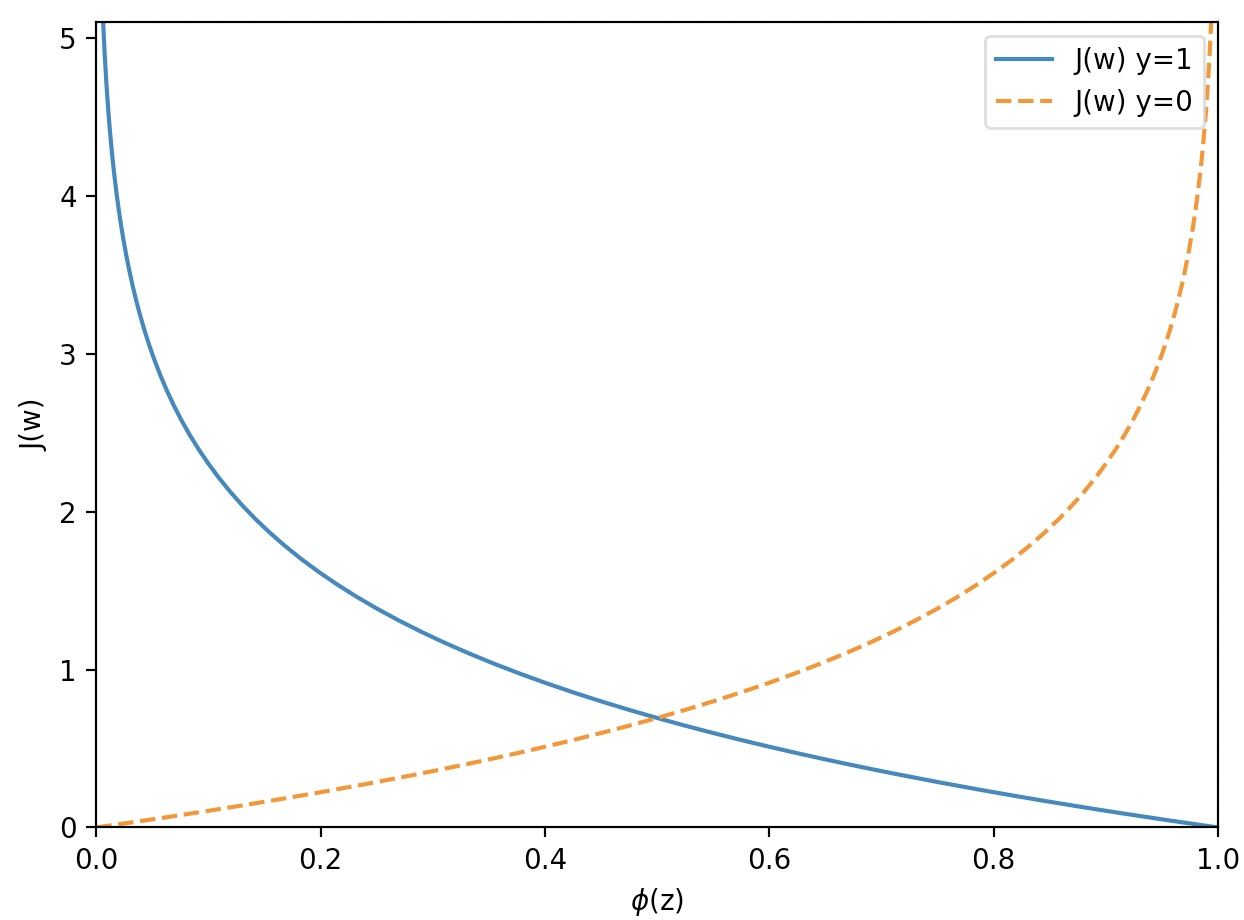
로지스틱 회귀의 비용함수
def cost_1(z):
return -np.log(sigmoid(z))
def cost_0(z):
return -np.log(1-sigmoid(z))
z=np.arange(-10, 10, 0.1)
phi_z=sigmoid(z)
c1=[cost_1(x) for x in z]
plt.plot(phi_z, c1, label='J(w) y=1')
c0=[cost_0(x) for x in z]
plt.plot(phi_z, c0, linestyle='--', label='J(w) y=0')
plt.ylim(0.0, 5.1)
plt.xlim([0,1])
plt.xlabel('$\phi$(z)')
plt.ylabel('J(w)')
plt.legend(loc='best')
plt.tight_layout()
plt.show()
LogisticRegreesionGD
class LogisticRegressionGD(object):
def __init__(self, eta=0.05, n_iter=100, random_state=1):
self.eta=eta
self.n_iter=n_iter
self.random_state=random_state
def fit(self, X, y):
rgen=np.random.RandomState(self.random_state)
self.w_=rgen.normal(loc=0.0, scale=0.01, size=1+X.shape[1])
self.cost_=[]
for i in range(self.n_iter):
n_input=self.net_input(X)
output=self.activation(net_input)
errors=(y-output)
self.w_[1:]+=self.eta*X.T.dot(errors)
self.w_[0]+=self.eta*errors.sum()
cost=(-y.dot(np.log(output))-((1-y).dot(np.log(1-output))))
self.cost_.append(cost)
return self
def net_input(self,X):
return np.dot(X,self.w_[1:])+self.w_[0]
def activation(self, z):
return 1./(1.+np.exp(-np.clip(z, -250, 250)))
def predict(self, X):
return np.where(self.activation(self.net_input(X))>=0.5, 1, 0)
위의 로지스틱 모델은 이진 분류 문제에만 적용할 수 있다.
X_train_01_subset=X_train[(y_train==0)|(y_train==1)]
y_train_01_subset=y_train[(y_train==0)|(y_train==1)]
lrgd=LogisticRegressionGD(eta=0.05, n_iter=1000, random_state=1)
lrgd.fit(X_train_01_subset, y_train_01_subset)
plot_decision_regions(X=X_train_01_subset, y=y_train_01_subset, classifier=lrgd)
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()
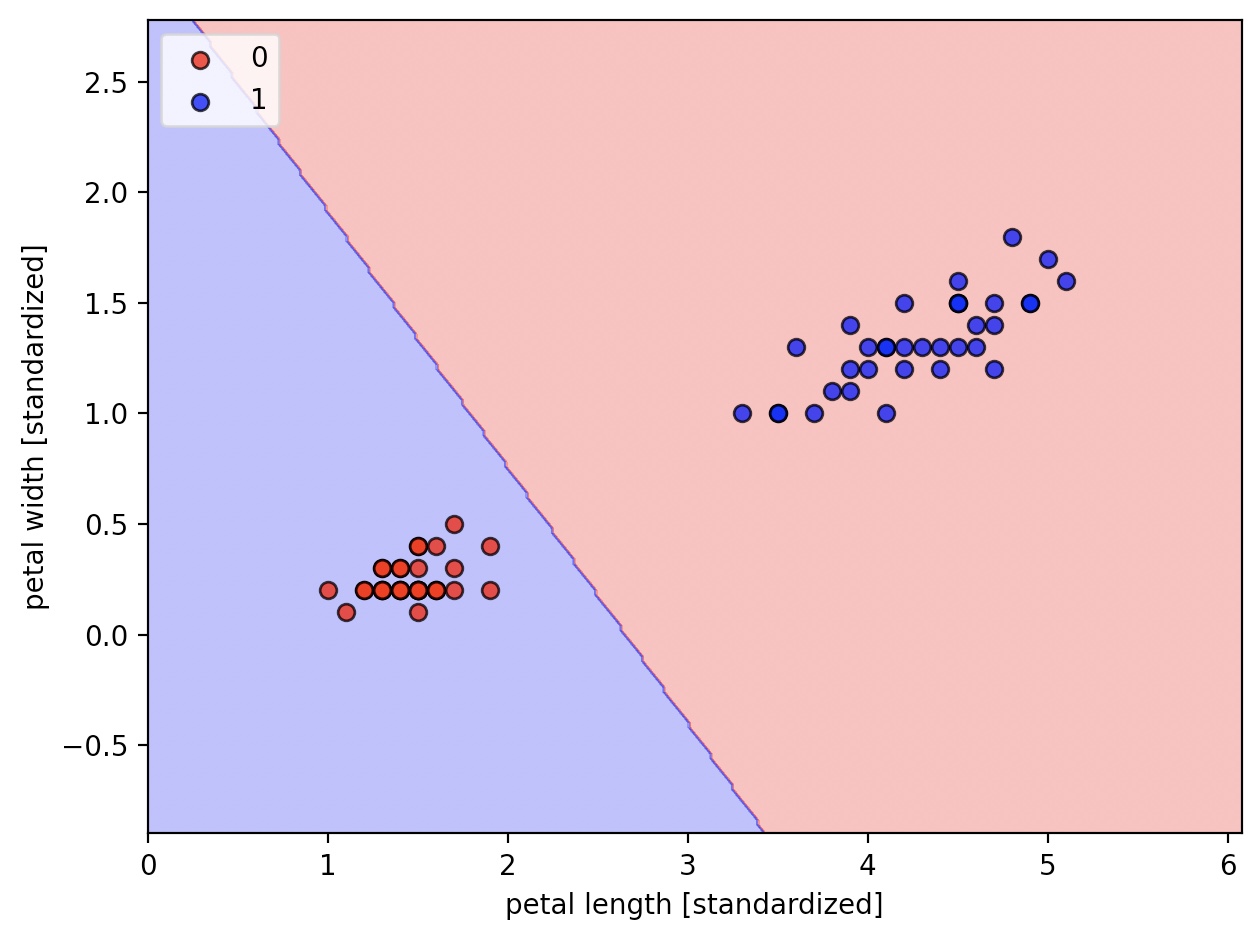
수학적으로 계산하여 보면, 로그 기능도를 최대화하는 것은 아달린의 비용함수를 최소화하는 것과 동일하다.
Logistic regression with Scikit-learn
사이킷런의 로지스틱 회귀 구현은 매우 최적화 되어 있고, 다중 분류도 지원한다.
from sklearn.linear_model import LogisticRegression
lr=LogisticRegression(C=100.0, random_state=1)
lr.fit(X_train_std, y_train)
plot_decision_regions(X_combined_std, y_combined, classifier=lr, test_idx=range(105,150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()
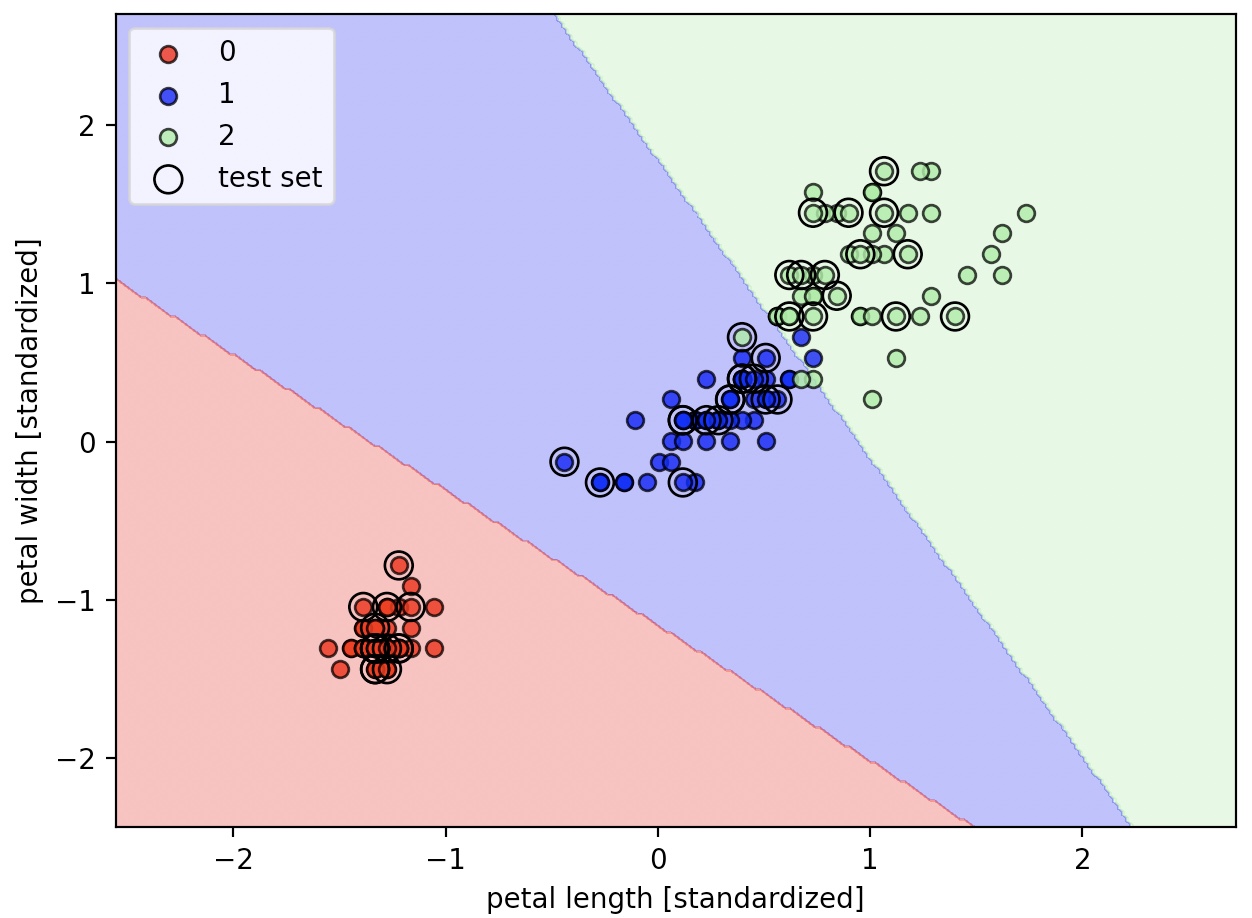
사이킷런은 로지스틱 회귀를 위한 다양한 최적화 알고리즘을 제공한다.
solver매개변수에 ‘newtoncg’, lbfgs’, liblinear’, ‘sag’, ‘saga’를 지정할 수 있다
매개변수 기본값은 auto로 이진분류이거나 solver=‘liblinear’DLF RUDDN ovr을 선택
그 이에는 multinomial을 선택한다.
클래스 소속 확률
lr.predict_proba(X_test_std[:3, :])
predict_proba 함수를 이용해서 어떤 클래스에 속할 확률을 계산할 수 있다.
위의 예시는 테스트 데이터셋에 있는 처음 세 개의 샘플 확률을 예측
array([[1.52213484e-12, 3.85303417e-04, 9.99614697e-01],
[9.93560717e-01, 6.43928295e-03, 1.14112016e-15],
[9.98655228e-01, 1.34477208e-03, 1.76178271e-17]])
행에서 가장 큰 값의 열이 예측 클래스 레이블이 된다.
lr.predict(X_test_std[:3, :]
array([2, 0, 0])
샘플 하나의 클래스 레이블을 예측할 때, 사이킷런은 입력 데이터로 2차원 배열을 기대한다.
따라서 하나의 행을 2차원 포맷으로 변경해줘야 한다.
lr.predict(X_test_std[0,:].reshape(1,-1))